Linux 内核已经合入了 EEVDF 调度器用于替代任职多年的 CFS 调度器。我对调度这种宏观且复杂的算法一直感到敬畏,还是先了解一下基本思路吧。
TL;DR
一句话总结就是:调度资源只会分配给 具有合格的(eligible)最早虚拟截止时间 调度请求 的任务。
引出问题
这部分和 EEVDF 基本无关,但这是作者认为调度需要解决的本质问题。
首先定义:
- \(w_i\):关联到任务 \(i\) 的权重。
- \(A(t)\):在时间点 \(t\) 时,处于活跃状态(正在竞争调度资源)的任务集合。
那么可以描述 \(f_i(t)\),表示时间点 \(t\) 时任务 \(i\) 的份额:
\[\begin{equation} f_i(t) = \frac{w_i}{\sum_{j \in A(t)}w_j} \tag{1} \end{equation}\]理想状态下,任务 \(i\) 在 \([t_0, t_1]\) 时间段内的应得服务时间为:
\[\begin{equation} S_i(t_0, t_1) = \int_{t_0}^{t_1}f_i(\tau)d\tau \tag{2} \end{equation}\]但是一个真实的调度器是实际处于离散状态,设 \(t_{0}^{i}\) 为任务 \(i\) 变为活跃状态的时间点,\([t_{0}^{i}, t]\) 内的实际服务时间为 \(s_i(t_{0}^{i}, t)\)。实际环境下由于调度开销等因素,与理想环境相比存在服务时间差距 \(lag\)。设时间点 \(t\) 时任务 \(i\) 服务时间差距为:
\[\begin{equation} lag_i(t) = S_i(t_{0}^{i}, t) - s_i(t_{0}^{i}, t) \tag{3} \end{equation}\]这里的核心问题就是怎么去处理 lag。
一些概念
EEVDF 是一种比例份额调度算法。而比例份额调度的特色在于每个任务都有权重的概念。不同的权重占比影响一个任务能获得调度资源的份额:比如存在 2 个任务,一个权重为 1,另一个权重为 3,那就分别能获得 25% 和 75% 的调度资源。
关于调度资源:在本论文中认为,如果一个任务想要获取调度资源,则需发出调度请求。
关于虚拟时间:可简单理解为经权重调整过的现实时间。这种概念在 CFS 调度器中也有应用,因为完全公平调度追求的是所有任务的虚拟运行时间相同,当一个任务权重更高(low nice),其虚拟时间流逝速度相比普通任务更慢,因此能在公平的意义下获取更多的实际运行时间。EEVDF 的用法基本一样,它统一了所有不同权重的任务的时间统计单位,同时可以轻易转换为现实时间:比如一个运行队列中只有 2 个任务,一个任务权重为 2,另一个权重为 3,那么系统的虚拟时间增速就是 \(\frac{1}{w_1+w_2} = \frac{1}{2 + 3} = 0.2\) 每秒,一个虚拟时间单位对应于 5 个现实时间单位。
关于截止时间:正如实时调度里的概念,就是最晚获得所有请求资源的时间点。作者用周期性调度举例,已知调度周期 \(T\),最大服务时间 \(r\),就是要求每个周期内都能拥有 \(r\) 的服务时间长度,因此资源份额有 \(f = \frac{r}{T}\)。反过来,已知请求创建的时间点 \(t\),其请求长度为 \(r\),其截止时间则是 \(t + \frac{r}{f}\)。
关于合格时间:这是 EEVDF 中独有的概念。在新的调度请求发出前,理论应得服务时间长度等同于现实已有服务时间长度,那么此时的时间点则是合格时间。这个定义使得在后续公式计算中关联上理论应得和实际已得的数值。
EEVDF 描述
在 EEVDF 算法中,通过结合公式 \((1)\) 和 \((2)\),得到活跃任务 \(i\) 在时间段 \([t_1, t_2]\) 应得服务时间:
\[\begin{equation} S_i(t_1, t_2) = w_i\int_{t_1}^{t_2}\frac{1}{\sum_{j \in A(\tau)}w_j}d\tau \tag{4} \end{equation}\]并且定义时间点 \(t\) 对应的虚拟时间 \(V(t)\):
\[\begin{equation} V(t) = \int_{0}^{t}\frac{1}{\sum_{j \in A(\tau)}w_j}d\tau \tag{5} \end{equation}\]再结合公式 \((4)\) 和 \((5)\) 得到在虚拟时间意义下的服务时间:
\[\begin{equation} S_i(t_1, t_2) = w_i(V(t_2) - V(t_1)) \tag{6} \end{equation}\]由于合格时间 \(e\) 的定义满足 \(S_i(t_{0}^{i}, e) = s_i(t_{0}^{i}, t)\),其中 \(t\) 为请求初始化的时间点(注意存在两种情况 \(e1 \le t\)或者\(e2 > t\),第一种情况就是 \(t\) 时间点立刻确认合格,第二种情况需要等待到 \(e2\) 时间点才算合格)。再结合使用公式 \((6)\) 可以描述虚拟合格时间:
\[\begin{equation} V(e) = V(t_{0}^{i}) + \frac{s_i(t_{0}^{i}, t)}{w_i} \tag{7} \end{equation}\]以及虚拟截止时间,其中 \(r\) 表示一个新请求的时间长度,即 \(S_i(e, d) = r\),再结合公式 \((6)\) 得到:
\[\begin{equation} V(d) = V(e) + \frac{r}{w_i} \tag{8} \end{equation}\]直到这一步,作者已经把现实时间的概念给抛弃掉,因为这些时间现在都可用虚拟时间来描述。
后面将用 \(ve\) 表示虚拟合格时间,\(vd\) 表示虚拟截止时间。由于每个请求都有 \(ve\) 和 \(vd\),再次定义:
- \(r^{(k)}\):由任务 \(i\) 创建的第 \(k\) 个请求的长度。
- \(ve^{(k)}\):上述请求对应的虚拟合格时间。
- \(vd^{(k)}\):上述请求对应的虚拟截止时间。
如果任务每次都完整使用了它请求到的服务时间,使用公式 \((7)\) 和 \((8)\) 可以得到:
\[\begin{equation} ve^{(1)} = V(t_{0}^{i}) \tag{9} \end{equation}\] \[\begin{equation} vd^{(k)} = ve^{(k)} + \frac{r^{(k)}}{w_i} \tag{10} \end{equation}\] \[\begin{equation} ve^{(k+1)} = vd^{(k)} \tag{11} \end{equation}\]如果任务并没有完整使用服务时间,那么相比上面只需改动公式 \((11)\),其中 \(u^{(k)}\) 表示在第 \(k\) 个请求中实际用到的服务时间:
\[\begin{equation} ve^{(k+1)} = ve^{(k)} + \frac{u^{(k)}}{w_i} \tag{12} \end{equation}\]可以看出这种情况下,后续的合格时间会被提前。
示例
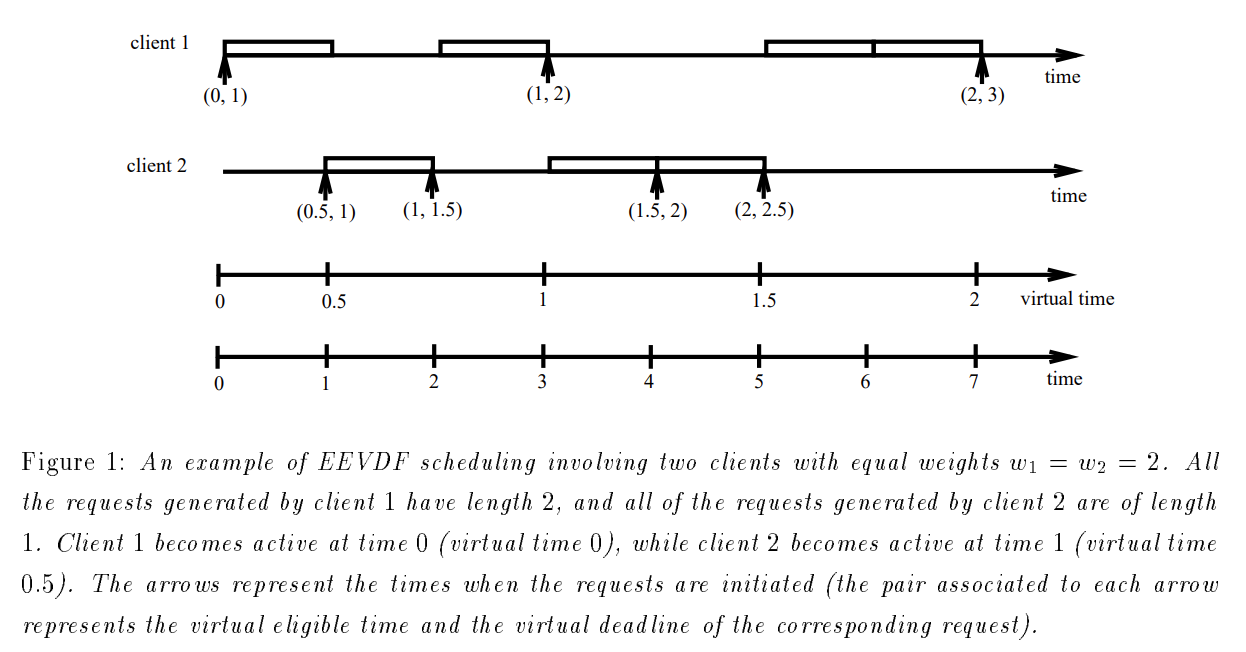
上面展示了 EEVDF 的一个示例。两个不同的任务(client),发出的请求长度为 \(r_1 = 2, r_2 = 1\)。
假设任务 1 在 \(t_0 = 0\) 时参与调度,根据公式 \((9)\) 和 \((10)\),\(ve = 0, vd = ve + \frac{r_1}{w_1} = 1\)。此时由于是只有单个任务且具有合格请求,因此获得调度资源(这里单次分配的资源是 time quantum,设为 1 秒)。
在 \(t = 1\) 时,任务 2 参与调度竞争。虚拟时间从现实时间 \([0, 1)\) 的增长速率是固定的(\(\frac{1}{w_1} = 0.5\)),由公式 \((5)\) 得到 \(V(1) = \int_{0}^{1}\frac{1}{w_1}d\tau = 0.5\),后续任务 2 加入后的增速改为 \(\frac{1}{w_1 + w_2} = 0.25\)。假设此时任务 2 也有了调度请求,此时共有 2 个待定请求:一个是来自任务 1 的虚拟截止时间为 1 的请求(在等待其它 time quantum 到来以“填满”请求);另一个是来自任务 2 的刚创建的请求,同样是虚拟截止时间为 1。这种请求任选其一,比如选择任务 2 的请求,因此第二个 time quantum 已经填满了任务 2 的当前请求,任务 2 现在可以发出一个新的请求,其中虚拟合格时间为 1,虚拟截止时间为 1.5。
在 \(t = 2\) 时,唯一合格的请求来自任务 1,因此它获得了下一个 time quantum。
在 \(t = 3\) 时,再次有两个合格的请求,但由于任务 2 的请求拥有比任务 1 新发出的请求更早的虚拟截止时间(\(vd_2 = 1.5 < vd_1 = 2\)),因此选择前者。
公平性
这部分会说明如何去更新 lag 和虚拟时间。
作者认为一个调度器需要满足以下三种操作:
- 让任务加入调度竞争。
- 让任务离开调度竞争。
- 修改任务的权重。
理想状态不存在 lag,而实际额外开销使得这三种操作均会产生 lag,这会影响到后续的公平性。
那怎么办?结论是:EEVDF 将 lag 也加入到虚拟时间的更新中来保证公平性。
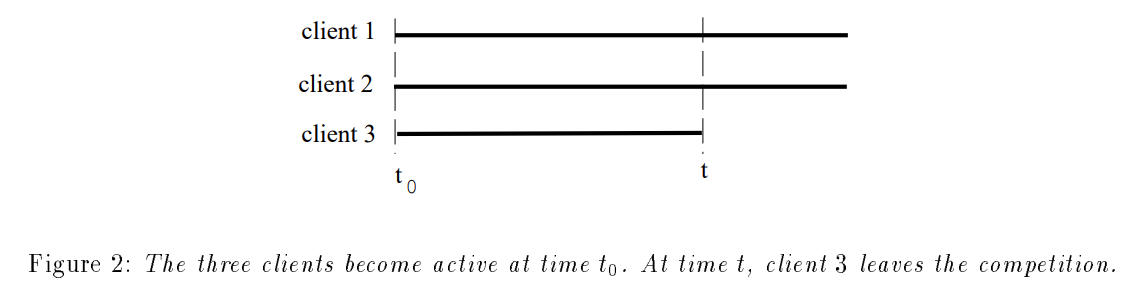
假设存在这种情况:三个任务从 \(t_0\) 开始参与调度竞争,但是 \(t\) 时间点任务 3 离开调度竞争。因为在 \([t_0, t)\) 时间段中,活跃任务的个数以及份额并没有发生改变,所以虚拟时间的增速是 \(\frac{1}{w_1 + w_2 + w_3}\)。并且使用公式 \((3)\) 可以算出:
\[\begin{equation} lag_i(t) = w_i\frac{t - t_0}{w_1 + w_2 + w_3} - s_i(t_0, t), i = 1,2,3 \tag{13} \end{equation}\]而剩下的两个任务已分配的服务时间可以通过 \(t - t_0 - s_3(t_0, t)\) 来表示。并使用 \(t^+\) 表示任务 3 离开竞争后的那一瞬间,忽略开销的话就是 \(t^+ \to t\)。那么 \(t^+\) 时刻任务 1 和任务 2 已接收多少服务时间呢?一个思路就是直接比例划分:
\[\begin{equation} S_i(t_0, t^+) = (t - t_0 - s_3(t_0, t))\frac{w_i}{w_1 + w_2}, i = 1,2 \tag{14} \end{equation}\]注意到 \(lag_3(t) \ne 0\),上面的式子并不等于离开前每个任务所接收服务时间(\((t-t_0)\frac{w_i}{w_1 + w_2 + w_3}\))。这是因为任务 3 离开后会等比例的丢失或增加服务时间。作者用该式子和 \((13)\) 将 \(s_3(t_0, t)\) 替换:
\[\begin{equation} \begin{aligned} S_i(t_0, t^+) &= (t - t_0)\frac{w_i}{w_1 + w_2 + w_3} + w_i\frac{lag_3(t)}{w_1 + w_2} \\ &= w_i(V(t) - V(t_0)) + w_i\frac{lag_3(t)}{w_1 + w_2}, i = 1,2 \end{aligned} \tag{15} \end{equation}\]接着使用 \((6)\) 和 \((15)\) 并去掉 \(w_i\) 权重可得到:
\[\begin{equation} V(t^+) = V(t) + \frac{lag_3(t)}{w_1 + w_2} \tag{16} \end{equation}\]因此,为了保证剩下任务的公平性,需要根据离开竞争的任务对应的 lag 来更新虚拟时间。同时作者认为 \(s_i(t_0, t) = s_i(t_0, t^+)\),再使用 \((3), (16)\) 可以算出前 2 个任务在 \(t^+\) 的 lag:
\[\begin{equation} \begin{aligned} lag_i(t^+) &= w_i(V(t^+) - V(t_0)) - s_i(t_0, t^+) \\ &= lag_i(t) + w_i\frac{lag_3(t)}{w_1 + w_2}, i = 1,2 \end{aligned} \tag{17} \end{equation}\]总结 \((16)\) 得出,当一个任务 \(j\) 在时间点 \(t\) 离开调度竞争时,对应的虚拟时间更新为:
\[\begin{equation} V(t) = V(t) + \frac{lag_j(t)}{\sum_{i \in A(t^+)}w_i} \tag{18} \end{equation}\]相应的,当一个任务 \(j\) 在时间点 \(t\) 加入调度竞争时,对应的虚拟时间更新为:
\[\begin{equation} V(t) = V(t) - \frac{lag_j(t)}{\sum_{i \in A(t^+)}w_i} \tag{19} \end{equation}\]得出一个结论:通过公式 \((18), (19)\) 来更新虚拟时间,可以保证所有活跃任务的 lag 之和为 0。
NOTE: 至于修改权重的操作那就是同时离开并加入:
\[\begin{equation} V(t) = V(t) + \frac{lag_j(t)}{(\sum_{i \in A(t)}w_i) - w_j} - \frac{lag_j(t)}{(\sum_{i \in A(t)}w_i) - w_j + w'_j} \tag{20} \end{equation}\]但是作者指出,如果一个(存在非零 lag 的)任务先离开调度竞争,后续再次加入回调度竞争(rejoin),那此时刻对应的 lag 的补偿(或惩罚)计算就没有简单的办法。
算法实现
前面提到对于 rejoin 这种行为没有好办法去处理公平性,作者给了三种策略:
- 如果任务在 \(t\) 离开,\(t'\) 重加,则 \(lag(t) = lag(t')\)。其它操作按照公式 \((18), (19), (20)\) 来计算。
- 类似上面的策略,但不同在于:离开竞争后,不再保留 lag,因此重加后 lag 也是 0。
- 只允许在 lag 为 0 的情况下执行加入、离开、修改操作,因此不需要更新虚拟时间。但是这种策略有它本身的复杂性,具体看论文吧……
论文后续有相关的代码实现以及复杂的公平性证明。个人感觉实现的部分可以直接从 Linux v6.6 入手(看论文就是为了这个!),所以这里就跳过了,感兴趣的读者请翻附录;证明部分应该没人愿意看的吧……我也不看这些的,再次跳了。
所以没有别的了,就这样吧,全文完。