布谷鸟过滤器(cuckoo filter)的实现挺有意思,花点时间看下论文是值得的。
为什么需要它?

布谷鸟过滤器解决了布隆过滤器(bloom filter)不支持删除操作的问题,同时具有低误报率、高空间利用率和缓存友好的特性。
Cuckoo hashing
开始之前先介绍下布谷鸟哈希(cuckoo hashing)算法。这个算法先说疗效:在不需要完美哈希的前提下,也可以做到最坏 \(O(1)\) 时间复杂度的查找操作。对比之下,常规哈希算法是期望 \(O(1)\),最坏 \(O(n)\) 的时间复杂度。因此这个特性对于高频读操作的场景来说是相当合适。
当然,这是有代价的,布谷鸟哈希的插入操作所需时间复杂度也和常规哈希相反:最坏 \(O(n)\),期望 \(O(1)\)。

布谷鸟哈希的实现恰如其名,就是鸠占鹊巢的过程。首先需要准备 2 个哈希表 \(T_1, T_2\),以及 2 个哈希函数 \(h_1, h_2\)。对于任意一个记录 \(x\),可以插入到 \(T_1[h_1(x)]\) 或者 \(T_2[h_2(x)]\)。如果对应位置已经存在另一个记录 \(y\),那就直接抢占,记录 \(y\) 需跳转到另一边的哈希表。如果这种操作在固定次数内没有完成,则会认为哈希表已满,需要 \(rehash\) 扩容。伪代码如下:
procedure insert(x)
if lookup(x) then return
loop MaxLoop times
x ↔ T1[h1(x)]
if x = ⊥ then return
x ↔ T2[h2(x)]
if x = ⊥ then return
end loop
rehash(); insert(x)
end
伪代码中
↔表示交换,⊥表示空记录。
由于记录 \(x\) 只可能存在于 \(T_1[h_1(x)]\) 或者 \(T_2[h_2(x)]\),因此查找操作的实现非常简单:
function lookup(x)
return T1[h1(x)] = x ∨ T2[h2(x)] = x
end
Optimized cuckoo hashing
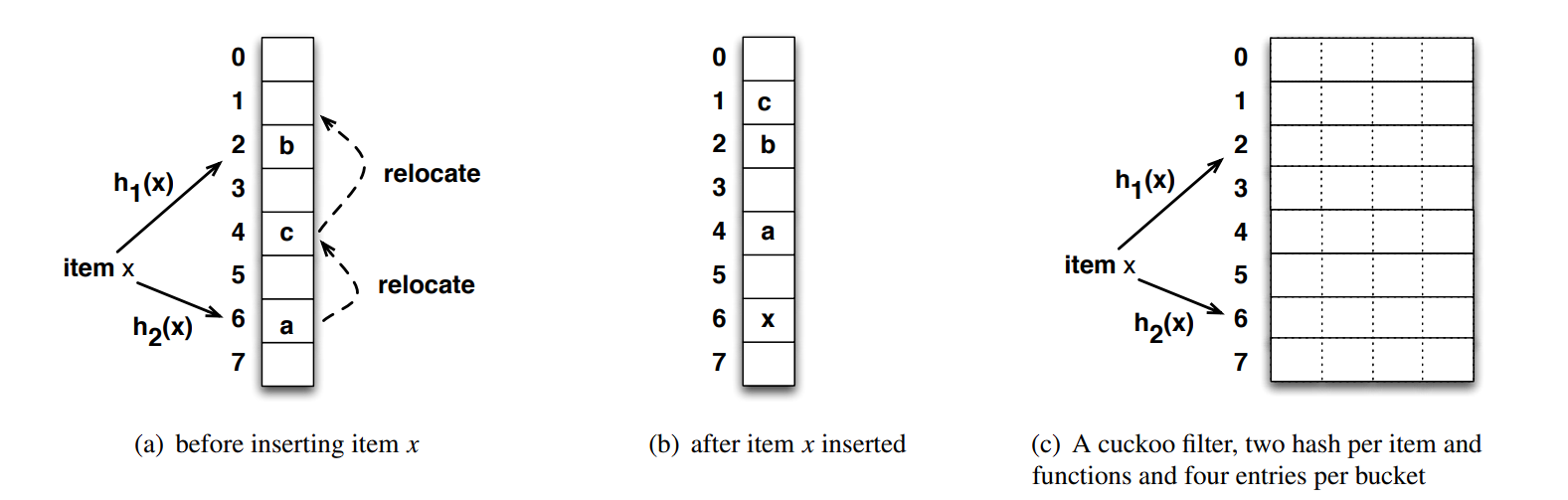
布谷鸟过滤器使用的布谷鸟哈希算法是经过改进的:
- 只使用一个哈希表。
- 并且使用多路哈希桶的结构。
- 表中存放指纹而非记录。
如上图 (c) 所示,哈希表由多个桶构成,每个桶中具有深度为 4 的条目,即可区分 4 个相同哈希值的记录。每个记录仍可定位到两个桶中,其下标为 \(h_1(x)\) 和 \(h_2(x)\)。
哈希表中并不再存放记录本身,而是只存放截取的指纹。指纹指的是经过特殊哈希截取的值,其宽度(如 8-bit,16-bit)取决于预期的误报率。
这种实现具有更高的空间利用率。在调优充分的情况下,可以做到高达 95% 的利用率。
Cuckoo filter algorithms
布谷鸟过滤器使用上述改进过的布谷鸟哈希算法是有问题需要解决的。前面提到它只存了指纹 \(f\),但是在标准布谷鸟哈希算法中,插入操作是需要保留原记录 \(y\) 才能进行“抢占巢穴”,因为需要重新定位被抢占方的备用巢穴 \(h_2(y)\),此时只依靠指纹 \(f\) 并不足以计算哈希值。
作者想到一个巧妙的思路去解决这个问题:使用部分键的布谷鸟哈希(partial-key cuckoo hashing)。对于每一个记录 \(x\),可以基于当前哈希值和指纹算出另一侧的哈希值:
h1(x) = hash(x)
h2(x) = h1(x) ⊕ hash(x’s fingerprint)
简单来说就是用了异或的性质:若 a xor b = c,反推得 c xor b = a。所以对于任意一个桶下标 \(i\),可以通过 \(j = i ⊕ hash(fingerprint)\) 得到另一个下标 \(j\)。此时插入操作不再需要保留原记录 \(x\):
Algorithm 1: Insert(x)
f = fingerprint(x);
i1 = hash(x);
i2 = i1 ⊕ hash(f);
if bucket[i1] or bucket[i2] has an empty entry then
add f to that bucket;
return Done;
// must relocate existing items;
i = randomly pick i1 or i2;
for n = 0; n < MaxNumKicks; n++ do
randomly select an entry e from bucket[i];
swap f and the fingerprint stored in entry e;
i = i ⊕ hash(f);
if bucket[i] has an empty entry then
add f to bucket[i];
return Done;
// Hashtable is considered full;
return Failure;
有一个小问题是为什么使用哈希过的指纹 \(j = i ⊕ hash(f)\),而不是直接使用指纹 \(j = i ⊕ f\)?这是因为指纹相比于下标来说可能是位数比较小的,考虑异或的性质会知道,这样的位置分布并不均匀,会大量集中在当前下标的周围(受限于 \(f\) 的宽度,高位并不会变化)。所以需要多加一步 \(hash(f)\)。
接下来的查找操作和删除操作就简单了,理解插入操作后应该无需解释。
Algorithm 2: Lookup(x)
f = fingerprint(x);
i1 = hash(x);
i2 = i1 ⊕ hash(f);
if bucket[i1] or bucket[i2] has f then
return True;
return False;
Algorithm 3: Delete(x)
f = fingerprint(x);
i1 = hash(x);
i2 = i1 ⊕ hash(f);
if bucket[i1] or bucket[i2] has f then
remove a copy of f from this bucket;
return True;
return False;
需要注意的是,删除操作只接受已插入的记录,这并不难理解。
最简实现
不考虑调优的话已经足以复现一个低配版的过滤器了。我也试写了一版最简实现,希望别嫌弃:
// 只是看论文简单复现的布谷鸟过滤器
// 实现上并不考虑所有情况
/// @brief A simple fixed-size cuckoo filter.
/// @tparam T Type of items.
/// @tparam N Size of cuckoo filter. Must Be a power of 2.
template <typename T, size_t N>
class Cuckoo {
/// Interfaces.
public:
Cuckoo() noexcept;
/// @brief Add an item to cuckoo filter.
/// @param item Any string.
/// @return Maybe false if no enough space.
bool add(const T &item) noexcept;
/// @brief Remove an item from cuckoo filter.
/// @param item Any added string.
void remove(const T &item) noexcept;
/// @brief Lookup an item from cuckoo filter.
/// @param item Any string.
/// @return True if found.
bool lookup(const T &item) const noexcept;
private:
/// @brief Fingerprint is 16-bit fixed.
using fbits = uint16_t;
/// @brief
/// UNSAFE magic code for checking null entry in bucket.
/// Obviously, this is not suitable for a normal cuckoo filter,
/// but it does make cuckoo algorithm simpler.
constexpr static fbits magic_code = 0x5a5a;
/// @brief STL-like npos.
constexpr static size_t npos = -1;
/// Core functions.
private:
/// @brief Generate a fingerprint for x.
/// @return A 16-bit fingerprint.
/// @todo Add any-bit fingerprint.
fbits fingerprint(const T &x) const noexcept;
/// @brief Hash value of fingerprint.
/// @param f Fingerprint.
/// @return A 64-bit remapped value, but restricted below N.
size_t hash(fbits f) const noexcept;
size_t hash(const T &x) const noexcept;
/// Helper functions.
private:
/// @brief buckets[i] has fingerprint f?
/// @return Return entry index or npos.
size_t bucket_has(size_t i, fbits f) const noexcept;
/// @brief buckets[i] has a hole?
/// @return Return hole-entry index or npos.
size_t bucket_has_hole(size_t i) const noexcept;
/// @brief Add an entry to bucket <del>randomly</del>.
/// @param i Bucket index.
/// @param e Entry index.
/// @param f Entry value (fingerprint).
void add_entry(size_t i, size_t e, fbits f) noexcept;
/// @brief Reset buckets[i][e] to null.
void reset_entry(size_t i, size_t e) noexcept;
/// @brief Return buckets[i][random()].
fbits& any_entry(size_t i) noexcept;
/// @todo Currently _buckets is fixed size.
void rehash() {}
private:
/// 4-way buckets.
/// TODO: Configurable multiway buckets.
fbits _buckets[N][4];
};
template <typename T, size_t N>
inline Cuckoo<T, N>::Cuckoo() noexcept {
static_assert(N == (N&-N), "Cuckoo needs a power of 2.");
for(auto &bucket : _buckets) {
std::fill(std::begin(bucket), std::end(bucket), magic_code);
}
}
template <typename T, size_t N>
inline bool Cuckoo<T, N>::add(const T &item) noexcept {
fbits f = fingerprint(item);
size_t i1 = hash(item);
size_t i2 = i1 ^ hash(f);
size_t itable[2] {i1, i2};
static bool s_round {};
/// Similar to a random choice.
if(s_round ^= 1) std::swap(itable[0], itable[1]);
/// About variables:
/// i - bucket index.
/// e - entry index.
/// entry - entry reference.
for(auto i : itable) {
auto e = bucket_has_hole(i);
if(e != npos) [[likely]] {
add_entry(i, e, f);
return true;
}
}
size_t i = itable[0];
for(size_t retry = 100; retry--;) {
auto &entry = any_entry(i);
std::swap(f, entry);
/// Cuckoo f has been added to entry.
/// Now we need to solve entry relocation (swapped into f).
i ^= hash(f);
auto next_e = bucket_has_hole(i);
if(next_e != npos) {
add_entry(i, next_e, f);
return true;
}
}
/// Hashtable is considered full.
return false;
}
template <typename T, size_t N>
inline void Cuckoo<T, N>::remove(const T &item) noexcept {
fbits f = fingerprint(item);
size_t i1 = hash(item);
size_t i2 = i1 ^ hash(f);
size_t itable[] {i1, i2};
for(auto i : itable) {
if(auto e = bucket_has(i, f); e != npos) {
reset_entry(i, e);
return;
}
}
assert(false);
}
template <typename T, size_t N>
inline bool Cuckoo<T, N>::lookup(const T &item) const noexcept {
fbits f = fingerprint(item);
size_t i1 = hash(item);
size_t i2 = i1 ^ hash(f);
return (bucket_has(i1, f) != npos) || (bucket_has(i2, f) != npos);
}
template <typename T, size_t N>
inline typename Cuckoo<T, N>::fbits Cuckoo<T, N>::fingerprint(const T &x) const noexcept {
constexpr size_t fbits_shift = sizeof(fbits) << 3;
constexpr size_t bitmask = ~(static_cast<size_t>(-1) << fbits_shift);
return std::hash<T>()(x) & bitmask;
}
template <typename T, size_t N>
inline size_t Cuckoo<T, N>::hash(fbits f) const noexcept {
/// FIXME: std::hash<*trivial*> returns f directly.
return std::hash<fbits>()(f) % N;
}
template <typename T, size_t N>
inline size_t Cuckoo<T, N>::hash(const T &x) const noexcept {
return std::hash<std::string>()(x) % N;
}
template <typename T, size_t N>
inline size_t Cuckoo<T, N>::bucket_has(size_t i, fbits f) const noexcept {
for(size_t j = 0; j < 4; ++j) {
if(_buckets[i][j] == f) return j;
}
return npos;
}
template <typename T, size_t N>
inline size_t Cuckoo<T, N>::bucket_has_hole(size_t i) const noexcept {
for(size_t j = 0; j < 4; ++j) {
if(_buckets[i][j] == magic_code) return j;
}
return npos;
}
template <typename T, size_t N>
inline void Cuckoo<T, N>::add_entry(size_t i, size_t e, fbits f) noexcept {
assert(_buckets[i][e] == magic_code);
_buckets[i][e] = f;
}
template <typename T, size_t N>
inline void Cuckoo<T, N>::reset_entry(size_t i, size_t e) noexcept {
_buckets[i][e] = magic_code;
}
template <typename T, size_t N>
inline typename Cuckoo<T, N>::fbits& Cuckoo<T, N>::any_entry(size_t i) noexcept {
static std::default_random_engine re{std::random_device{}()};
std::uniform_int_distribution<size_t> dis{0, 3};
size_t e = dis(re);
assert(_buckets[i][e] != magic_code);
return _buckets[i][e];
}
感兴趣可以看下完整测试,里面的数据规模约一百万(随机生成和 GPT 生成):Caturra000/Snippets/Algorithm/cuckoo_filter.cpp – Github。
虽然复现简单,但是在实现时仍需要注意一些细节:
- 过滤器容器的大小建议按照 \(N = 2^n\) 设计。因为在插入操作时涉及到 \(i ⊕ j\) 计算,即使保证了 \(i < M, j < M\),也可能 \(i ⊕ j \ge M\)。按幂设计有高位保证,可以简单避免问题。
- 标准库
std::hash不适合作为哈希函数\(h(f)\),比如libstdc++实现为直接映射,即 \(x \to x\)。